どうも、制作部 夏目です。
今日はみなさんご存知のDA PUMPのUSAの歌詞に出てくる一節の
「Pacific Oceanひとっ飛び〜」について疑問に思ったことがあるので、それについて書いていきたいと思います。
2:08あたりでこんなことを言っているんですね。
Pacific Oceanひとっ飛び〜
そこで理系魂に火がついてしまいまして、Pacific Oceanをひとっ飛びするために必要な初速度を求めてみようと思ったわけです。
それを求める中で出てくる滞空時間、最高到達点も紹介していきます。
前提条件
まずは、前提条件から定めていきます。
これがないと、計算が複雑になりますので、ご容赦ください m(_ _ )m
もし余力がある人は自分で計算してみてください ♩\(°w°)/♩
1.重力は高度によらず一定
2.外力は重力のみ
3.空気抵抗は一切無視する
4.空気摩擦による熱も考慮に入れない
5.物体の運動は斜方投射とする
6.打ち上げ角度は45°(45°が一番飛ぶ )
7.推進力は初速度v0のみ
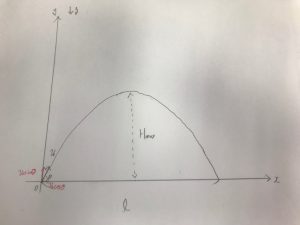
図を書くとこんな感じになります
初期条件
次に初期条件ですが、これは位置と速度で必要となりますが、以下のように定めます
位置の初期条件
x(0) = 0
y(0) = 0
速度の初期条件
vx(0) = v0 cosθ
vy(0) = v0 sinθ
それでは、計算レッツラゴー!
まずは、運動方程式は以下の2式で与えられる。
m d^2x/dt^2 = 0
m d^2y/dt^2 = -mg
これをガリガリと解いていく(積分する)と
dx / dt = vx(t) = C1 (C1は積分定数)
dy / dt = vy(t) = C2 – g * t (C2は積分定数)
先ほどの初期条件から
vx(0) = C1 = v0 * cosθ
vy(0) = C2 = v0 * sinθ
さらにもう一度積分することで
x(t) = v0 * t * cosθ + C3
y(t) = v0 * t * sinθ – 0.5 * g * t * t + C4
これも初期条件から
x(0) = C3 = 0
y(0) = C4 = 0
となります。
ので最終的に
速度と位置の運動方程式は以下のようになります。
vx(t) = v0 * cosθ
vy(t) = v0 * sinθ – g * t
x(t) = v0 * t * cosθ
y(t) = v0 * t * sinθ – g * t * t * 0.5
さて、ここからが本題です。
Pacific Ocean ひとっとび〜
と言っていますが、これを仮に東京-サンフランシスコ間であると仮定しましょう。
こちらのサイトによりますと、東京-サンフランシスコ間の距離は約8,280kmとのことなので、
体重m[kg]の人が、約8,280km離れた場所にひとっ飛びするのにかかる初速度v0,かかる時間t,最高到達点Hmaxは以下の式で与えられます。
v0 = √( g * l / ( sinθ * cosθ ) ) (1)
t = v0 * v0 * sinθ * cosθ / g (2)
Hmax = v0 * v0 * sinθ * sinθ / ( 2 * g ) (3)
(1)より
ここで
l:(東京-サンフランシスコ間の距離):8,280km = 8.280 * 10^6m
v0:初速度
θ:45°
g:重力加速度(≒9.8 m / s / s)
であるので初速度を求めてみると
v0 = √( g * l / ( 2 * cos(45°) * sin(45°)))
ここで
cos(45°) = sin(45°) = √2 / 2 ≒ 0.717
より、
v0 = 9000 [m/s]
なんとマッハ26.5もの速度で打ち出さないと、太平洋を横断することはできないということですね。
さらにこの時体にかかる負荷を計算(1秒間あたりの加速度を求めて、重力加速度で割る)すると
920Gということで人間が人間の姿を保てないほどの負荷が与えられるということがわかりました。
また、この旅行をするのにかかる時間を(2)と先ほど得た初速度から計算すると
t = 4,131405sとなり、なんと25時間40分近く空中にいることが明らかになりました。
この旅行中の最高到達点Hmaxを(3)と初速度、時間から求めてみると
なんと
1,748,411km(約175万km)ということで
ここからだと、月(地球-月の距離はおよそ38万km)のはるか上空まで到達できるみたいですね。
なんか軽い気持ちで計算してみましたが、結構えぐい結果となって驚いてます。
面白いと思ったら、いいねシェアよろしくです。
それでは次回の記事でお会いしましょう。
過去の記事はこちらから